A study on Error Detection and Efficiency in Matched Filters

Matched filters are used to identify parts of signal streams to segmented, pre-defined patterns. In this study, different patters of matched filters are compared and measured for their speed and effectiveness. The filters are applied to Automatic Dependence Surveillance - Broadcasting (ADS-B) signals, where their effectiveness can be easily measured. In addition, the test is carried out via MATLAB simulation for easy reproduction.

Background

Matched filters are an application of the convolution sum, an impulse response function between two time invariant or time variant signals. The convolution sum is described from [1]:

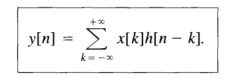
Where y[n] is the output signal in discrete time, x[k] is the nonshifted input signal, and h[n-k] is the shifted (by n) unit impulse function. A matched filter applies this convolution sum over a long range.

Matched filters are often used to compare a signal with added noise to its sterile counterpart. If noise is truly white, then the matched filter response to a noisy signal is clearly maximized [2].

Matched filters are also used to detect propagation delay with a sounding signal. In all cases, white and random noise performs far better than patterned noise [2].

The matched filter function comes from convolution of course, but also comes from probability density. The function follows a simple hypothesis test. The null hypothesis is that only noise was received in a random order; conversely, the alternative hypothesis is that the SNR is much greater and the desired signal is present. Matched filters are not exact but show a general trend of pattern-matching.

Application: ADS-B

Automatic Dependent Surveillance-Broadcast (ADS-B) is a type of pulse-position modulation (PPM) transmission that sends aircraft information mid-flight, to include GPS location, flight telemetry, and aircraft specifications [3]. ADS-B was chosen for this application because of its simplicity in the PPM signal and its simplistic error correction; a “correct” byte could be looked up on the internet for verification, such as [4].

This project specifically borrowed its research aim from [5], and used its prerecorded data streams as a failsafe for known addresses. This was chosen for redundancy, as the focus on matched filter application precipitated a known set of data to compare. However, this research does not follow strictly on the lab procedures outlined in [5]. Our MATLAB code automatically thresholds the signal and decodes it fully, which was only an extension offered by the lab manual.

ADS-B contains a preamble (introductory binary bits) and message text. The preamble is 8 microseconds long, while the message is 56 or 112 microseconds long. The message is manchester encoded, meaning, in this case, that only the odd bits count in binary logic [6]. For example, the oversampled data [00 01 10 11] interprets solely to [0 0 1 1]. To detect the entire ADS-B signal, it is easiest to only detect the preamble. The preamble is two spikes within an 8 microsecond transmission and are easily identifiable as shown below:

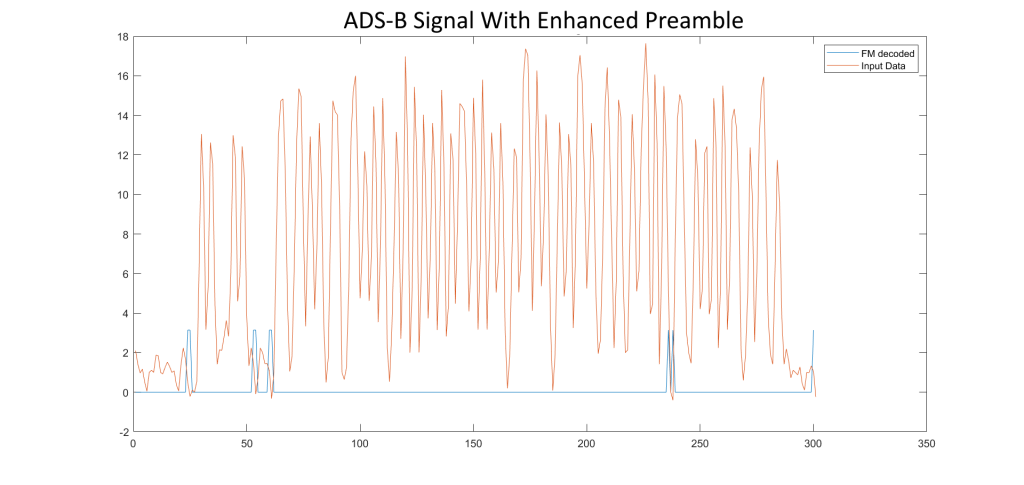
Note two spikes near beginning of signal.

ADS-B shows challenges with decoding because of various transmitter power and transmission capabilities. Extensions such as [6] attempt to enhance speed and strength in decryption.

Experimental Process

In this experiment, two base signals were used in a matched filter. The first signal was a vector of 1’s; a rectangular signal 112 microseconds long. The second was only the preamble at 8 microseconds long. Both versions ran off of the same MATLAB script to reduce variability. The matlab function conv(u,w) was used as a matched filter, with u being the input signal and w being the unit impulse. Below is a graph of the difference between the two filters:

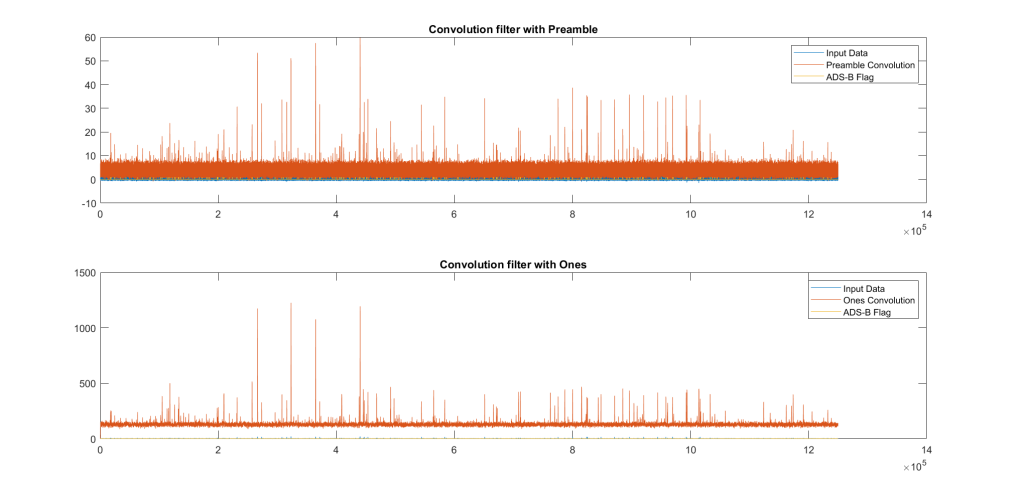
In this setup, the 1’s filter (bottom) has less random noise on the top of the modulated signal, but signal 1 (top) seems to have more peaks.

Both codes were run back-to-back with only small modifications between them. The code is available here. The 1’s filter acts as only a “squelch” on the signal; it reads high whenever a strong signal is present. The preamble filter actually reads through the input data as a reversed matched filter and produces a result.

w = conv(d, ones(1,128)); %Ones filter
w = w(1:length(d));
idx = w > 200;

%Preamble matched filter
Preamble = [1,0,1,0,0,0,0,1,0,1,0,0,0,0,0,0];
Preamble = Preamble.';
w = conv(d, Preamble); %128 us is the length of a packet
w = w(1:length(d)); %truncate it to length of d
idx = w > 10; %threshold

Efficiency / Error Correction

Due to websites such as [5], it is relatively easy to assess the success of each script. The 1’s filter completed operation in 4.936 seconds. It produced 386 ICAO addresses, and 14 DATA fields for its input IQ signal stream. However, only part of the ICAO addresses were usable - near 80%. Further, only 4/14 of the DATA fields returned actual results. This does not disprove the results, but frames them; DATA fields are not always transmitted and can have false positives.

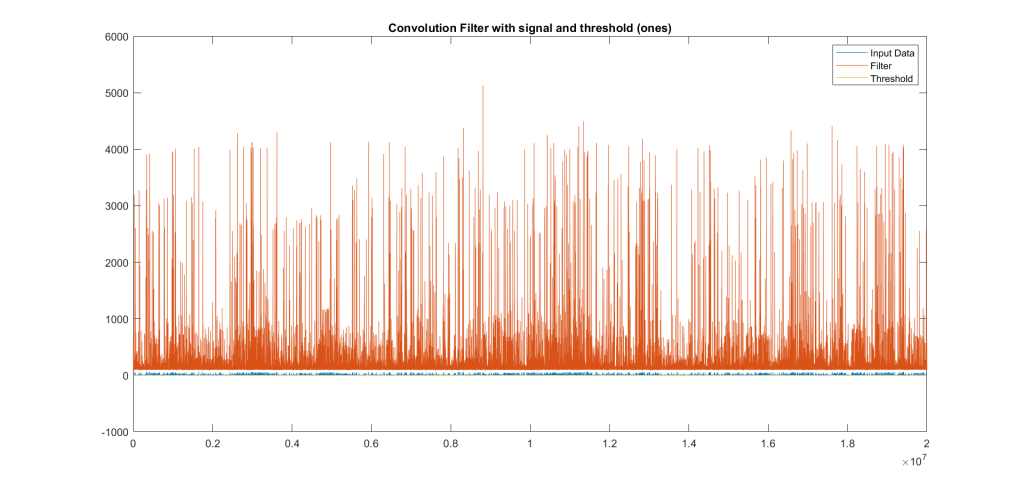
ones filter

The Preamble matched filter, surprisingly, returned 2,699 results in 6.595 seconds. However, these results had several duplicates and can only be trusted to about 75%, or about 2000 results. Further, the DATA field had 7 usable fields excluding duplicates. However, the presence of many duplicates strengthened the case for these signals; if they appeared multiple times on the detection then they are most likely a valid signal. The study made an assumption that every aircraft on the DATA list was a valid flightpath, considering the data may be old and flights may have changed airports or typical destinations in recent years.

Preamble Filter

Conclusion

Although the “squelch” design of a matched filter with ones produces meaningful results quickly, it fails to reach the depth of the preamble-focused matched filter. Different applications may call upon different designs, but a structured matched filter, even for basic pulse position modulation , will be preferred to find averaging of a signal.

Further studies must incorporate [3] and [6] for more in-depth exploration and design of tailored matched filters. Moving averages would improve SNR for each received signal. Futher, the ADS-B decryption can be created in real-time using other signal processing software, such as GNU Radio. Overall, a specific matched filter in ADS-B applications produce more meaningful and thorough responses to an input stream.

Sources

[1]. Oppenheim et al. Signals and Systems: Chapter 2. 2nd edition. Prentice Hall NJ. 1996.

[2]. Turin, George L. “An Introduction to Matched Filters.” IEEE, IRE Transactions on Information Theory. 1960.

[3]. Zou et al. “An S Mode ADS-B Preamble Detection Algorithm.” IEEE, 2019 International Conference on Computer and Communications.

[4]. Flightaware. Flight Tracker. https://flightaware.com/

[5]. Gill, John, and Broad, Nicholas. EE179: Final Project. Stanford. http://web.stanford.edu/class/ee179/labs/LabFP_ADSB.html

[6]. Ren et al. “Novel Error Correction Algorithms for ADS-B Signals with Matched Filter Based Decoding.” Physical Communication. 11 January 2019.